How is sample size calculated? Are there systematic guidelines on how to determine sample size? This article explains how to calculate sample size.
How do you determine the sample size required for your specific study? This is an important question, considering that the answer determines how much effort you should devote to your research, as well as how much money you have to allocate for it. This article explains how sample size should be estimated to get the optimal sample size.
As you would not want to sacrifice accuracy for convenience, and to make your research worthwhile, having the correct sample size makes your research more credible. If you sample too little, your results may not be reliable. If you sample too large a size, you will also spend too much.
Sampling is especially true to quantitative studies, as it tries to define or describe a population by studying a part of it. But how many should be enough?
Here are important considerations when estimating the correct sample size.
How to Find Sample Size: 4 Parameters
Statisticians agree that you have to be familiar with at least four things before you draw a sample from your population. These are enumerated and described below.
1. Size of the Population
As a researcher, you should be familiar with your target population’s size. It is therefore necessary that you define your population so that you can approximate or find ways to estimate the total population and get the optimal size possible.
Let’s say you would want to find out the tourists’ average willingness to pay to access or see a natural park in view of estimating the value of the natural park’s aesthetic value. This means that your population should be the number of tourists who visit the park in one year if you are discussing an annual turnout of visitors. You can get this number from the tourism office, especially if park access is for a fee.
Since you cannot interview all the tourists, a sample may be drawn at a certain point in time which you will determine yourself, bearing in mind the peak and the off seasons to avoid bias. Familiarity with your population, therefore, is a must.
2. Margin of Error or Confidence Interval
Margin of error refers to the range of values that are acceptable to you as you estimate of the population’s mean or average value. What is the percentage of error that you will allow to give you the level of confidence you need? Whatever value you get in estimating say, the mean of your population is not an absolute number. You should allow for little deviations that are statistically acceptable and serve your purpose.
An analogy to illustrate the margin of error is like a hunter trying to hit a deer with his arrow. He aims for the heart, but in the process hits the areas within 3 inches of the heart, either below, above, at the left or at the right. That is okay, because what he really wants is to bring the deer home for his meal. Hitting the parts surrounding the heart serves the purpose of going home with the booty. Hitting the lungs or the other internal parts next to the heart can immobilize it.
3. Confidence Level
Confidence level is a bit confused with margin of error. This is your level of certainty that your estimated mean (the statistic) will fall within the confidence interval that you have set for the estimate.
Again, back to the analogy of hitting the deer with an arrow. The question is, “How confident is the archer in hitting the areas surrounding the heart?” If he is really a very good archer, he might say that out of 100 arrows, he is certain that 95 of this would hit the area within 3 inches of the heart. That’s his confidence level or percentage of certainty.
In statistics, the convention is to have a confidence level of either 95% or 99%. The former is a commonly used standard.
Assuming that your population has a normal distribution, the confidence level corresponds to a value of the z-distribution. A z-distribution is a standard normal distribution, meaning—the population approximates a bell-shaped curve.
4. Standard Deviation
The standard deviation is how spread out the numbers are from the mean. To make this concept clear, let’s go back to the hunter example.
Let’s say the hunter shot a target with a bullseye 500 times. As he is a very good archer, most of the arrows would have landed near or at the center, but for sure, not always at the center. Those arrows that missed the bullseye are like the deviations from the mean. The way the arrows spread from the center indicates deviations from the average.
So how far will the arrows released by the hunter deviate from the center? We don’t know unless we measure the distance of each of the arrows from the center. But we don’t have time to measure all the 500 arrows he released, so we might as well take a sample, say 20 arrows. Those 20 arrows might show that the deviation from the bullseye is within 4 inches. So this value can predict the deviation of the 500 arrows consequently released.
Getting the population standard deviation from 20 samples is analogous to a pilot study of the population. A portion of the population may be studied to estimate the population’s standard deviation. If it is not possible to do so, it is common practice that a standard deviation of 0.5 is used in estimating sample size.
The population standard deviation is computed by getting the square root of the variance. The variance is the average of the squared differences from the mean. This is denoted by the formula given below:
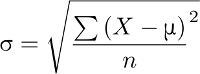
How is Sample Size Calculated?
Using Confidence Level, Standard Deviation and Margin of Error to Estimate the Sample Size
If you are now ready with at least three measures to estimate sample size, i.e., margin of error, confidence level and standard deviation, then you are now ready to estimate the sample size you need. For example, let’s have the following data:
Given:
Confidence level
2.326 (the corresponding value in the z table indicating 99% of the population is accounted for)
Standard deviation
0.5 (assuming that the population standard deviation is unknown)
Margin of error
5% or 0.05
The following equation is used to compute the sample size:
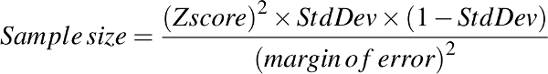
Substituting given values to the equation:
Sample size = ((2.326)² x 0.5 x (1-0.5))/(0.05)²
= (5.4103 x 0.25)/ 0.0025
= 1.3526/0.0025
= 541.04 ~ 541 (always round up to the higher integer number)
Therefore, if your research requires interviewing people, the estimated number of interviewees is 541.
How to Calculate Sample Size Using Online Resources
If you want a straightforward, quick estimate of sample size without going through the detailed computation given in the preceding discussion, you may just use a sample size table. See the Sample Size Table prepared by Research Advisors as your guide.
Similarly, you can use Survey Monkey’s Sample Size Calculator ->.
Simple does it.
But of course, you need to understand how is sample size calculated so that whatever you get from these calculators would make sense to you.
Having a good background on how the sample size was derived guards you from erroneously making a spurious sample size estimate leading to potentially questionable conclusions.
References
Niles, R. (n.d.). Standard deviation. Retrieved on 18 February 2015 from http://www.robertniles.com/stats/stdev.shtml
Smith, S. (2013). Determining Sample Size: How to Ensure You Get the Correct Sample Size. Retrieved on 19 February 2015 from http://www.qualtrics.com/blog/determining-sample-size/
©2015 February 22 P. A. Regoniel; updated June 21, 2022
[cite]

