Probability and Statistics for Graduate Research

Probability and Statistics in Graduate Study

Many graduate students approach probability and statistics with a sense of unease — especially when they open their textbook and encounter an entire chapter on probability. You might wonder, “Why do I need to learn this? I just want to conduct my research.”

Here’s the truth: probability isn’t just theory — it’s the foundation of how we make decisions with data. If you want your research to stand on solid ground, you must understand how probability supports statistical reasoning and how it applies to your own projects.

What Is Probability and Statistics in Research Terms?

Section 1: Probability

At its core, probability is simply the measure of how likely something is to happen. In research, it helps us quantify uncertainty — because every study, no matter how carefully designed, involves variability.

Probability is the measure of how likely something is to happen.

Think of probability as a bridge between data and conclusions: it tells you how confident you can be that your results reflect reality rather than random chance.

The Classic Coin Toss to Illustrate Probability

Let’s revisit the most basic example of probability: a coin toss.

• A fair coin has two sides: heads and tails.
• When tossed, there’s an equal chance — 50% each — that it will land on either side (although there’s a highly unlikely chance that it will land on its side as once happened to me).

In statistics, we write this as:
p = 0.5

where p stands for probability.

If you toss the coin 10 times, you’d expect around 5 heads and 5 tails. If you toss it 100 times, you’d expect about 50 of each.

But here’s the important part for your research: Probability doesn’t guarantee outcomes; it expresses expectations. You might toss 10 coins and get 7 heads — and that’s not “wrong” or “unlucky.” It’s simply the natural variability of real-world data.

This same principle applies when you run an experiment: the numbers will fluctuate. Probability helps you figure out whether those fluctuations are just random noise — or whether they reflect a real effect worth paying attention to.

---

From Coins to Research Questions: Why Probability Matters

Suppose you want to know if remedial classes improve student performance. You divide students into two groups:

• Group A: students who took remedial classes
• Group B: students who did not

You test them afterward and compare scores.

Here’s where probability steps in. When you see a difference in scores, you must ask:

Is this difference real — or could it have happened by chance?

This is the heart of statistical analysis.

---

The Role of the p-value (and Why Everyone Talks About 0.05)

When you run a test like a t-test, the software will produce a p-value — a number between 0 and 1.

• The p-value tells you the probability of observing your data (or something more extreme) if there really were no effect — in other words, if your null hypothesis were true.

For our remedial class study, your hypotheses might look like this:

• Null hypothesis (H₀): There is no difference in test scores between students who took remedial classes and those who didn’t.
• Alternative hypothesis (H₁): There is a difference in test scores between the two groups.

If your p-value is 0.05, that means there’s a 5% chance that the difference you see could simply be random.

If the p-value is lower than 0.05, researchers typically take that as evidence strong enough to reject the null hypothesis — concluding that the difference is probably real.

---

Why This Matters for Your Graduate Research

Graduate research isn’t about memorizing formulas — it’s about designing studies that produce meaningful, trustworthy results. Understanding probability helps you:

1. Choose the right statistical tests – because each test is based on assumptions about probability.
2. Interpret your p-values correctly – so you don’t overstate or understate your findings.
3. Design stronger studies – by planning for sample sizes that reduce random noise and increase reliability.

For instance, if you’re testing a new teaching method, probability thinking will guide you to:

• Decide how many students you need to include.
• Understand that some variation in scores is normal.
• Avoid drawing conclusions from differences that could easily have happened by chance.

---

Key Points to Remember in Designing Your Research

1. Probability isn’t abstract math — it’s how we measure uncertainty in research.
2. A p-value is a probability statement — it tells you how likely your results would appear if your hypothesis of “no effect” were true.
3. Statistical significance (p ≤ 0.05) doesn’t mean your finding is “important” — it means the observed result is unlikely to be due to chance alone.
4. Your study design matters as much as your analysis — bad design can’t be fixed by good statistics.

Gain Confidence as a Graduate Student

As a graduate student, you don’t need to become a mathematician — but you do need to become a thoughtful consumer of data. Getting a good grasp of probability will help you ask better questions, design stronger studies, and draw conclusions you can defend with confidence.

When you see that “p = 0.03” in your research output, you’ll know exactly what it means — and, just as importantly, what it doesn’t mean.

That’s when statistics stops being intimidating — and starts becoming one of your most powerful research tools.

---

Section 2: How Statistics Builds on Probability

If probability is the foundation, then statistics is the structure built on top of it.

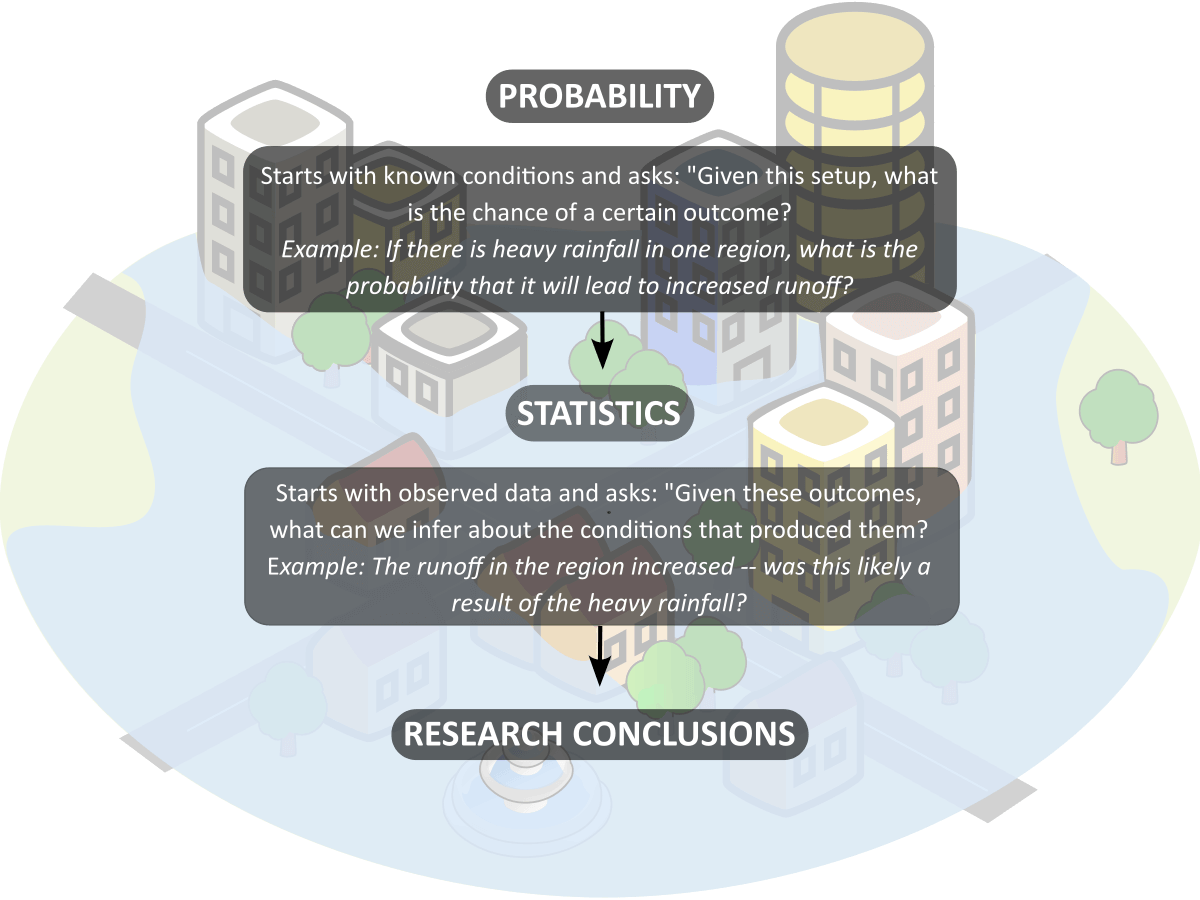
• Probability starts with known conditions and asks:
  “Given this setup, what is the chance of a certain outcome?”
  (Example: If I flip a fair coin 100 times, how many heads should I expect?)
• Statistics starts with observed data and asks:
  “Given these outcomes, what can we infer about the conditions that produced them?”
  (Example: I flipped a coin 100 times and got 60 heads — is the coin really fair?)

This relationship matters for your research because statistical tests are built on probability models.

Statistical tests are built on probability models.

When you run a t-test, ANOVA, regression, or chi-square test, the software is comparing what you observed in your study to what probability theory says you should observe if the null hypothesis were true.

Here’s the connection step by step:

1. Probability gives the rules.

It tells us what “random variation” looks like — e.g., how much scores might fluctuate even if there’s no real difference.

2. Statistics applies those rules to real-world data.

It asks: Are these observed differences so large (or so consistent) that they are unlikely to have happened by chance alone?

3. The p-value ties it all together.

That single number reflects a probability calculation based on your statistical test.

For example:

• In a t-test, probability distributions describe how the difference between two group means might behave by chance.
• In multiple regression, probability helps determine whether the slope of a line (the relationship between variables) is likely to be real or random.
• In ANOVA, probability models show how much of the variation in your data can be explained by group differences versus random error.

Why This Connection Matters for Graduate Research

Bearing in mind that statistics = probability in action helps you see that statistical software isn’t “magic.”

When SPSS, R, or Excel gives you a p-value, it’s not just crunching numbers blindly — it’s using probability theory to evaluate your data against a mathematical model.

This mindset helps you:

• Select the right statistical test for your design.
• Understand why assumptions (like “normal distribution” or “equal variance”) matter — they’re the probability rules your test relies on.
• Avoid common mistakes like saying “p = 0.03 proves my hypothesis” (it doesn’t — it simply shows that your data would be unlikely under the null model).

Enjoy your quantitative data analysis venture. It’s time you love analyzing data and discover the excitement of finding correlations and differences that you can share with the world.

©Patrick Regoniel | Updated 29 July 2025

---